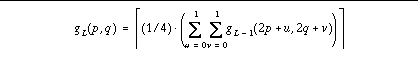Search Algorithms for Block-Matching in Motion
Estimation
Deepak Turaga, Mohamed Alkanhal
Mid-Term project
18-899
Spring, 1998
Interframe predictive coding is used
to eliminate the large amount of temporal and spatial redundancy that exists
in video sequences and helps in compressing them. In conventional predictive
coding the difference between the current frame and the predicted frame
(based on the previous frame) is coded and transmitted. The better the
prediction, the smaller the error and hence the transmission bit rate.
If a scene is still, then a good prediction for a particular pel in the
current frame is the same pel in the previous frame and the error is zero.
However, when there is motion in a sequence, then a pel on the same part
of the moving object is a better prediction for the current pel. The use
of the knowledge of the displacement of an object in successive frames
is called Motion Compensation. There are a large number of motion compensation
algorithms for interframe predictive coding. In this study, however, we
have focused only on one class of such algorithms, called the Block Matching
Algorithms. These algorithms estimate the amount of motion on a block by
block basis, i.e. for each block in the current frame, a block from the
previous frame is found, that is said to match this block based on a certain
criterion. There are a number of criteria to evaluate the "goodness" of
a match and some of them are:
1. Cross Correlation Function
2. Pel Difference Classification (PDC)
3. Mean Absolute Difference
4. Mean Squared Difference
5. Integral Projection
Some of these criteria are simple to
evaluate, while others are more involved. Different kinds of algorithms
use different criteria for comparison of blocks. One of the first algorithms
to be used for block based motion compensation is what is called the Full
Search or the Exhaustive Search. In this, each block within a given search
window is compared to the current block and the best match is obtained
(based on one of the comparison criterion). Although, this algorithm is
the best one in terms of the quality of the predicted image and the simplicity
of the algorithm, it is very computationally intensive. With the realization
that motion compensation is the most computationally intensive operation
in the coding and transmitting of video streams, people started looking
for more efficient algorithms. However, there is a trade-off between the
efficiency of the algorithm and the quality of the prediction image. Keeping
this trade-off in mind a lot of algorithms have been developed. These algorithms
are called Sub-Optimal because although they are computationally more efficient
than the Full search, they do not give as good a quality as it.
There are several approaches to reducing
the computational complexity. For instance there are the Signature Based
Algorithms that reduce the computation by using several stages, in each
of which a different comparison criterion is used. In the first stage all
the blocks are evaluated using a computationally simple criterion and then
based on the results of this stage a subset of the candidates is picked
for the next stage, where a more complex criterion is used. There are algorithms
that exploit the limitations of the human observers. These algorithms reduce
computational complexity by reducing the candidates that are chosen for
the comparison, based on the knowledge that the human eyes cannot perceive
fast motion with full resolution. So they use what is called a coarse quantization
of vectors i.e. around the centre of the search area all blocks are evaluated
as potential matches,
while far from the centre only a subset of blocks is
considered. This idea is illustrated in the following figure.
Fig 1: Example of coarse quantization of vectors
Some algorithms are based on the nature
of the image data than the limitations of the human observers. It is believed
by these algorithms that very good matches are likely to be found in the
vicinity of reasonably good matches. Although this assumption might not
be necessarily true, it is useful for reducing the computation as the search
can be broken down into stages where the algorithm successively narrows
down on the regions of good matches. There are a large number of algorithms
that make this assumption and these may be classified as algorithms based
on the Principle of Locality. One of the problems with these algorithms
is that they can converge to a local minimum rather than to the global
minimum. These algorithms can be modified by changing the manner in which
the algorithm narrows down the search area. For instance the extent of
reduction of the search area can be made a function of the two smallest
distortions in the previous stage, rather than just the smallest distortion.
Such algorithms are called the Dynamic search Window algorithms.
There is another class of algorithms,
that seeks to exploit the natural spatial dependency (homogeneity) that
exists in most images. Hence the motion vector for a block can be predicted
based on the motion vectors of the blocks surrounding it. One can also
exploit temporal dependency by trying to predict the motion vectors for
the current block based on the motion vectors for the same block from the
previous frame. There are other approaches to the problem like the Hierarchical
motion vector estimation using the Mean Pyramid where the image is broken
down into lower resolution components and the motion vectors for this lower
resolution image are computed and propagated down the pyramidal structure
of better and better resolution images.
On the whole there are a very large
number of algorithms for block based motion compensation. This report includes
a study of some of the main algorithms. We have tried to implement some
of these and the results are discussed.
2.0 Search Algorithms
In this section we will discuss ten
block-based search algorithms.
2.1 Three Step Search (TSS) [1,2]
This algorithm was introduced by Koga
et al in 1981. It became very popular because of its simplicity and
also robust and near optimal performance. It searches for the best motion
vectors in a coarse to fine search pattern. The algorithm may be described
as:
Step 1: An initial step size is picked. Eight blocks at
a distance of step size from the centre (around the centre block) are picked
for comparison.
Step 2: The step size is halved. The centre is moved to
the point with the minimum distortion.
Steps 1 and 2 are repeated till the
step size becomes smaller than 1. A particular path for the convergence
of this algorithm is shown below:
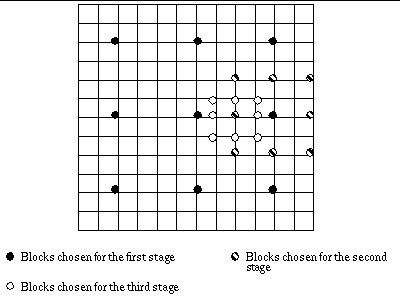
Fig 2 : Example path for convergence of Three Step Search
One problem that occurs with the Three Step Search is
that it uses a uniformly allocated checking point pattern in the first
step, which becomes inefficient for small motion estimation.
2.2 Two Dimensional Logarithmic Search (TDL) [1]
This algorithm was introduced by Jain
& Jain around the same time that the Three Step Search was introduced
and is closely related to it. Although this algorithm requires more steps
than the Three Step Search, it can be more accurate, especially when the
search window is large. The algorithm may be described as :
Step 1 : Pick an initial step size. Look at the block at
the Centro the search are and the four blocks at a distance of s from this
on the X and Y axes. (the five positions form a + sign)
Step 2 : If the position of best match is at the centre,
halve the step size. If however, one of the other four points is the best
match, then it becomes the centre and step 1 is repeated.
Step 3: When the step size becomes 1, all the nine blocks
around the centre are chosen for the search and the best among them is
picked as the required block.
A particular path for
the convergence of the algorithm is shown in the following figure:
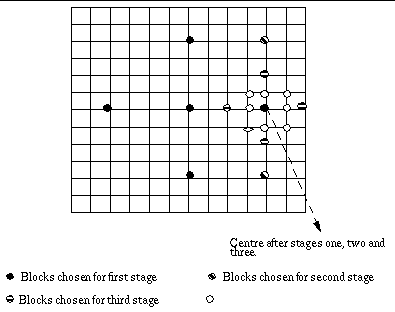
Fig 3: Example path for convergence
of Two Dimensional Logarithmic Search
A lot of variations of this algorithm
exist and they differ mainly in the way in which the step size is changed.
Some people argue that the step size should be halved at every stage. Some
people believe that the step size should also be halved if an edge of the
search space is reached. However, this last idea has been found to fail
sometimes.
2.3 Binary Search (BS) [3]
This is also one of the algorithms
that are very popular for motion estimation and in fact it is used for
motion estimation by MPEG-Tool. The basic idea behind this algorithm is
to divide the search window into a number of regions and do a full search
only in one of these regions. It may be described as :
Step 1 : The MAD is evaluated on a grid of 9 pixels
that include the centre, the four corners of the search window and four
pels at the boundaries. The search window is divided into regions based
on these points.
Step 2: A full search is performed in the region corresponding
to the point with the smallest MAD.
The convergence of the algorithm may
be viewed in figure 4. The pels that lie between the dashed lines are never
considered. Hence, although the Binary search requires fewer comparisons
(the worst case scenario for this search window is 33 comparisons), it's
performance is not very good because of this zone of pixels that are never
considered.
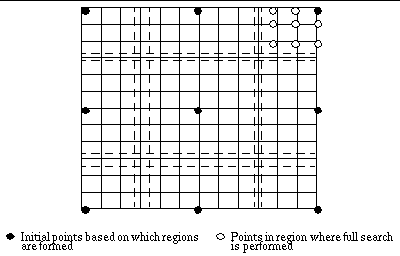
Fig 4 : Example path for convergence
of Binary Search
2.4 Four Step Search (FSS) [3]
This algorithm was proposed in 1996
by Lai-Man Po and Wing-Chung Ma. It is based on the real world image sequence's
characteristic of centre-biased motion. The algorithm starts with a nine
point comparison and then the other points for comparison are selected
based on the following algorithm:
Step 1: Start with a step size of 2. Pick nine points around
the search window centre. Calculate the distortion and find the point with
the smallest distortion. If this point is found to be the centre of the
searching area go to step 4, otherwise go to step 2.
Step 2 : Move the centre to the point with the smallest
distortion. The step size is maintained at 2. The search pattern, however
depends on the position of the previous minimum distortion.
a) If the previous minimum point
is located at the corner of the previous search area, five points are picked
(as shown in the figure).
b) If the previous minimum distortion point is located
at the middle of the horizontal or vertical axis of the previous search
window, three additional checking points are picked. (as shown in the figure)
Locate the point with the minimum distortion. If this is
at the centre, go to step 4 otherwise go to step 3.
Step 3 : The search pattern strategy is the same, however
it will finally go to step 4.
Step 4: The step size is reduced to 1 and all nine points
around the centre of the search are examined.
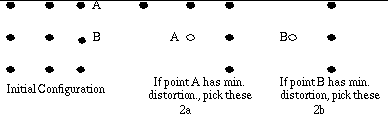
Fig 5 : Illustration of selection of blocks for different
cases in Four Step Search
The computational complexity of the
four step search is less than that of the three step search, while the
performance in terms of quality is as good. It is also more robust than
the three step search and it maintains its performance for image sequences
with complex movements like camera zooming and fast motion. Hence it is
a very attractive strategy for motion estimation.
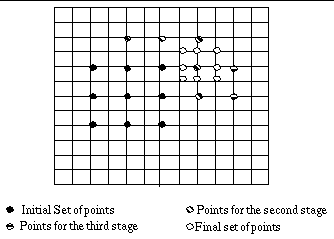
Fig 6: Example path for convergence of Four Step Search.
2.5 Orthogonal Search Algorithm (OSA) [1]
This algorithm was introduced by Puri
in 1987 and it is a hybrid of the Three Step Search and the Two Dimensional
Logarithmic Search. It has a vertical stage followed by a horizontal stage
for the search for the optimal block. Than algorithm may be described as
follows :
Step 1 : Pick a step size (usually half the maximum displacement
in the search window). Take two points at a distance of step size in the
horizontal direction from the centre of the search window and locate (among
these) the point of minimum distortion. Move the centre to this point.
Step 2 : Take two points at a distance step size from the
centre in the vertical direction and find the point with the minimum distortion.
Step 3: Halve the step size, if it is greater than one,
else halt.
A particular path for the convergence of the algorithm
may be shown in the following figure.
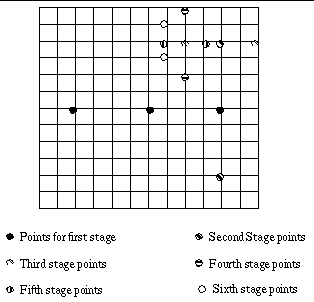
Fig 7 : Example path for convergence of Orthogonal Search
2.6 One at a Time Algorithm (OTA) [1]
This is a simple, but effective way
of trying to find a point with the optimal block. During the horizontal
stage, the point on the horizontal direction with the minimum distortion
is found. Then, starting with this point, the minimum distortion in the
vertical direction is found. The algorithm may be described as follows
:
Step 1 : Pick three points about the centre of the search
window. (horizontal)
Step 2 : If the smallest distortion is for the centre point,
start the vertical stage, otherwise look at the next point in the horizontal
direction closer to the point with the smallest distortion (from the previous
stage) Continue looking in that direction till you find the point with
the smallest distortion. (going in the same direction, the point next to
it must have a larger distortion)
Step 3: Repeat the above, but taking points in the vertical
direction about the point that has the smallest distortion in the horizontal
direction.
One particular search path for the algorithm is shown in
figure 8. This search algorithm requires very little time, however the
quality of match is not very good.
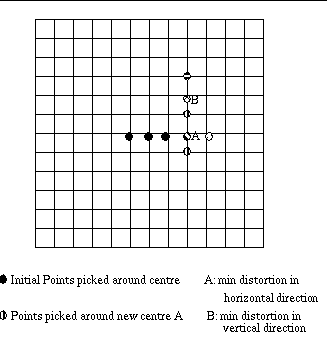
Fig 8 : Example path for convergence of One at a Time
Algorithm
2.7 Cross Search Algorithm (CSA) [1,4]
This algorithm was introduced by M.
Ghanbari in 1990. The basic idea in this algorithm is still a logarithmic
step search, however, the main difference between this and the logarithmic
search method presented before is the search locations picked are the end
points of a "x" rather than a "+". The algorithm may be described as follows
:
Step 1 : The centre block is compared with the current
block and if the distortion is less than a certain threshold, the algorithm
stops.
Step 2 : Pick the first set of points in the shape of a
"x" around the centre. (The step size picked is usually half the maximum
displacement) Move the centre to the point of minimum distortion.
Step 3 : If the step size is bigger than 1 halve it and
repeat step 2, otherwise go to step 4
Step 4 : If in the final stage the point of minimum distortion
is the bottom left or the top right point, then evaluate distortion at
4 more points around it with a search area of a "+". If, however, the point
of minimum distortion is the top left or bottom right point, evaluate the
distortion at 4 more points around it in the shape of a "x".
A probable search path for the
algorithm is shown in figure 9. The cross search algorithm requires 5 +
4 log2w comparisons, where w is the largest allowed displacement. The
algorithm has a low computational
complexity. It is, however, not the best in terms of compensation.
Fig 9: Example path for convergence
of Cross Search Algorithm.
2.8 Spiral Search (SS)
[3]
The spiral search algorithm
was proposed by Zahariadis and Kalivas in 1995. It seeks to combine the
ideas of the Three Step Search and the Binary search. By doing so, it tends
to not only speed up the computation, but also removes the problem of the
Binary search, where there is a zone of pixels that is never evaluated.
The algorithm may be described as follows:
Step 1 : The step size is picked
to half the maximum displacement in the search window. The point of minimum
distortion is found from among the nine points picked in the following
manner. Five points are picked in the shape of a "+" around the centre
of the search window (at a distance of step size in the vertical and horizontal
directions) The remaining four points are picked at the corners of the
search window.
Step 2 : The step size is reduced
and a search is performed around the point with the smallest distortion.
This is repeated till the step size falls to 1.
A probable search path for
the algorithm may be shown in figure 10. The spiral search does not outperform
the Four step search, however this search gives performance (in terms of
quality) comparable to the Three step search, with lesser computational
complexity.
Fig 10: Example path for
convergence of Spiral Search
2.9 Hierarchical Search
Block Matching Algorithms
To reduce the complexity
of the motion search algorithms, course-to-fine hierarchical searching
schemes have been suggested. This reduction in the computation is due to
the reduced image size at higher level. An example of these schemes is
the mean pyramid[5].
In the mean pyramid methods,
different pyramidal images are constructed by subsampling. Then a hierarchical
search motion vector estimation proceeding from the higher level to the
lower ones reduces the computational complexity and gets high quality motion
vectors. To remove the effects of noise at higher level, image pyramids
are constructed by using a low pass filter. A simple averaging is used
to construct the multiple-level pyramidal images: where gL(p,q) represents
the gray level at the position (p,q) of the Lth level and g0(p,q) denotes
the original image. The truncation is represented by | |. The construction
of mean pyramid by simple nonoverlaping low pass filtering is done by assigning
a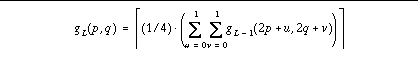
mean gray level of pixels
in a low pass window to a single pixel at the next level. The truncated
mean value of four pixels at the lowe level is recursively used in generating
mean pyramid. We have implemented this algorithm using three levels. One
pixel at level 2 corresponds to a 4 x 4 block and 2 x 2 block at level
0 and 1, respectively. Therefore, a block of size16 x 16 in level 0 is
replaced by a one of size 16/2L x 16/2L in level L. After construction
of mean pyramid, these images can be searched using the three step search
(TSS) where the motion vectors are searched at level 2 with MAD (Minimum
Absolute Difference) and the motion vector having the smallest MAD is selected
as the coarse motion vector at that level. That is the detected motion
vector at the higher level is transmitted to the lower level and it guides
the refinement step at that level. This motion estimation process is repeated
once more down to level 0, However more improvements have been done on
the TSS to make it more suitable for the Hierarchical structure[5].
Since MAD's are computed
at the highest level based on relatively small blocks, almost the same
values are likely to appear at several points. Thus to solve this problem,
[5] suggested to use more than one candidates at the highest level (level
2 for our special case). A number of motion vectors at level 2 are propagated
to the lower one. Full search with tow pixel resolution in a small window
around the candidates is used at level one to find the minimum difference
location as the a search centre at layer 0. Figure 11 shows search locations
of the algorithm.
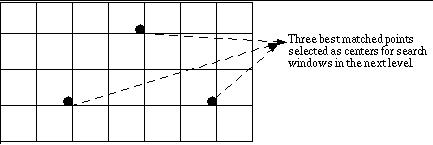
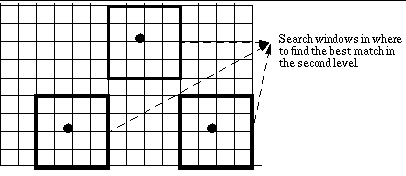
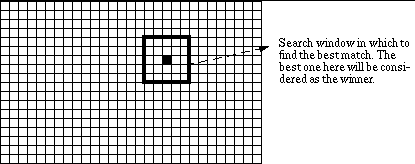
Fig. 11 Search locations
for the hierarchical search algorithm
2.10 Spatially Dependent
Algorithms
Spatial dependency check
the correlation between the motion vectors of neighboring blocks to provide
a prediction to the previous matching algorithms.Frequently the prediction
is formed by taking a weighted average of the neighboring motion vectors.
A typical block has eight immediate neighbors. Depending on the order in
which target blocks are matched, the motion vectors for some of these neighbors
might not been available when a block is being matched.
The hierarchical solution
used in the previous section has been modified by adding an additional
candidate in level 2 based on spatial correlation. In [6], it was suggested
to calculate the spatially dependent motion vector from neighboring motion
vectors. Let MVC be the motion vector of the current block, and MV1, MV2
and MV3 be the motion vectors of the neighboring blocks. To estimate MVC,
The motion vectors of the neighboring are examined and find a proper a
group out of five groups given in Fig. 12. Then, the corresponding shaded
block motion vectors are averaged and down-scaled to obtain an estimate
of MVC, which is the third candidate beside the other candidates that were
driven using the previous algorithm. In the case of group E where no motion
similar motion vectors exist, (0., 0) is selected as the estimate.
Fig. 12 Grouping of similar
neighboring motion vectors (MVs) to predict MVc
Here, e1=|| MV1 - MV2 ||,
e2=|| MV2 - MV3||, and e3=||MV3-MV1||, and D is threshold value to examine
similarity between the two MVs. A value of 8 for D has been used in our
simulations based on [2].
3.0 Experimental Results
and Discussion
Fifteen test sequences were
used for simulation. Seven of them, come only in QCIF format, while the
other four come in CIF and QCIF format.
Six algorithms, Full Search
(FS), Three Step Search (TSS), Two Dimensional Logarithmic Search (TDL),
Four Step Search (FSS), One at a Time Search Algorithm(OTA), Orthogonal
Search Algorithm (OSA), Mean Pyramid (MP) and the Improved Mean Pyramid
using Spatial Correlation (IMPSC) were implemented and compared based on
two measures. These measures are CPU time and the Averaged Minimum Absolute
Distance (AMAD). AMAD used to show algorithm quality while the CPU time
used for computational complexity.
Here, we show only the results
of testing seven streams for easy comparisons. First Search Algorithms
included here for comparison reason, since it is the optimal one in term
of quality.
In general, in terms of speed,
the OTA is the best one. On the other hand, its quality is in the worst
positions among these algorithms. The TDL came after OTA in terms of speed
and quality. As it can be seen, TSS achieves a small improvement in the
AMAD but it needs a big computational complexity comparing to the OTA.
While FSS outperforms the TSS in terms of speed, its quality does not approach
that of FS as the hierarchical algorithms (MP and IMPSC). Although the
speed of the MP and IMPSC is worst than some of other algorithms, they
outperform any other algorithm in terms of quality and they almost have
the same quality of the FS. The spatial information used in IMPSC increases
its speed comparing to the MP.
From the above, it's clear
that some of the algorithms are good in speed but they suffered in terms
of quality. We believe that the hierarchical algorithms came in the middle
between the FS and the locality based algorithms. Hierarchical algorithms
introduced the same quality as of the FS, and they reduced the computational
complexity greatly. The reason for the performance degradation, compared
to the FS, of algorithms based on the quadrant monotonic assumption is
due to finding the local minimum rather than the global one. The several
candidate motion vectors introduced by the MP and used in IMPSC reduces
the possibility of getting in a local minimum.
In this report, different
algorithms were presented and discussed. We implemented and compared most
of them based on some test streams. Our evaluation was based on two measures,
CPU time for computational complexity and AMAD for quality. As it is mentioned
in the last section, it's believed that the hierarchical algorithms succeeded
on maintaining the same quality of the Full Search and reducing the computational
complexity. However, we are not sure about the AMAD as a reasonable measure.
We are also not sure as whether a difference in AMAD represented by a difference
of, say, 0.2 really translated to a large difference in perceptual quality.
Another important measure that we need to consider in our future work is
the bit stream. This measure will help us evaluate the performance of our
algorithms, because ultimately these are the things that are being sent
over the communication line. We also intend to continue looking at different
types of algorithms and working toward exploring new directions. We might
try to combine the hierarchical approach with other fast search methods
such as FSS and OSA to further reduce computations with little degradation
on the quality.
1. http://atlantis.ucc.ie/dvideo/contents.html .
2. Lai-Man Po, Wing-Chung Ma "A Novel Four Step Search
Algorithm For Fast Block Motion Estimation" IEEE Transactions on Circuits
and Systems for Video Technology, vol. 6, no.3, pp 313-7, June 1996.
3. Th. Zahariadis, D. Kalivas "A Spiral Search Algorithm
For Fast Estimation Of Block Motion Vectors" Signal Processing VIII, theories
and applications. Proceedings of the EUSIPCO 96. Eighth European Signal
Processing Conference p.3 vol. lxiii + 2144, 1079-82,vol. 2.
4. M.Ghanbari "The cross search algorithm for Motion Estimation"
IEEE Transactions on Communications, vol. 38, no. 7 pp 950-3, July 1990.
5. Kwon Moon Nam, Joon-Seek Kim, Rae-Hong Park "A Fast
Hierarchical Motion Vector Estimation Algorithm Using Mean Pyramid" IEEE
Transactions on Circuits and Systems for Video technology, vol. 5, no.4,
pp 344-351, August 1995.
6. Kyoung Won Lim, Jong Boem Ra "Improved Hierarchical
Search Block Matching Algorithm by Using Multiple Motion Vector Candidates"
Electroonic Letters, vol. 33, no.21, pp 1771- 1772, October, 1997.